Výpis souhrnů
Logické výrazy
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Logické výrazy
V tomto tématu pracujeme s logickými výrazy s formálním značením (např. A or B), přičemž některé logické spojky značíme pomocí anglických slov (and, or, not). Toto značení je v informatice běžné, používá se například v mnohých programovacích jazycích. Téma dělíme na následující podtémata:
- Logické spojky a pravdivostní tabulky – význam jednotlivých logických spojek, přepisování z běžného jazyka do informatické notace (and, or, not, xor, ⇒, ⇔)
- Vyhodnocování logických výrazů – vyhodnocení složených výrazů kombinujících více logických spojek
- Úpravy logických výrazů – přepis na ekvivalentní výraz, který vypadá jinak, ale má vždy stejnou pravdivostní hodnotu
- Logické odvozování s výrazy – odvozování závěrů z předpokladů, kterých může být i více
Práci s logickými výroky si můžete dále procvičit i v různých jiných zápisech:
- Logické výroky slovy – výroky v běžném jazyce
- Logika na Umíme matiku – práce s výroky v matematické notaci (∧,∨,¬)
- Logické výrazy v Pythonu – práce s logickými výrazy v kontextu programování
Logické spojky a pravdivostní tabulky
Pravdivostní hodnoty
V informatice používáme většinou zaměnitelně následující:
- 1 = true = pravda
- 0 = false = nepravda
Logické spojky
| Zápis | Název | Význam |
|---|---|---|
| \text{ not } X | negace | neplatí X |
| X \text{ and } Y | konjunkce, a zároveň | X a Y platí současně |
| X \text{ or } Y | disjunkce, nebo | platí alespoň jedno z X a Y |
| X \text{ xor } Y | exkluzivní nebo | platí právě jedno z X a Y |
| X \Rightarrow Y | implikace, jestliže-pak | pokud platí X, pak platí i Y |
| X \Leftrightarrow Y | ekvivalence, právě když | X platí právě tehdy, když platí Y |
Pravdivostní tabulka logických operací
| X | Y | X \text{ and } Y | X \text{ or } Y | X \text{ xor } Y | X \Rightarrow Y | X \Leftrightarrow Y |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
Vyhodnocování logických výrazů
Vyhodnocení logického výrazu si můžeme představit jako zjištění, jestli je pravdivý nebo nepravdivý. U jednoduchého výroku jeho vyhodnocení odpovídá jeho pravdivosti, ale u složitějších výroků s logickými spojkami jde o kombinaci pravdivostí jednotlivých podvýroků pomocí spojek.
Například spojka and se vyhodnotí na pravdu (true, 1) právě tehdy, když jsou oba výroky pravdivé.
Tedy 1 and 1 = 1, ale například 1 and 0 = 0.
Pravdivostní tabulka logických operací
| X | Y | X \text{ and } Y | X \text{ or } Y | X \text{ xor } Y | X \Rightarrow Y | X \Leftrightarrow Y |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
Úpravy logických výrazů
Úpravy logických výrazů je vhodné provádět například tehdy, když chceme určit pravdivost daného výroku nebo porovnat, jestli jsou dva výroky shodné. K tomu se hodí základní přepisová pravidla.
Přepis základních logických spojek
| Výrok | Ekvivalentní výrok |
|---|---|
| \text{not not } X | X |
| \text{not } (X \text{ and } Y) | (\text{not } X) \text{ or (not } Y) |
| \text{not }(X \text{ or }Y) | (\text{not } X) \text{ and (not } Y) |
Přepis implikace, ekvivalence a operace xor
| Výrok | Ekvivalentní výrok |
|---|---|
| X \Rightarrow Y | (\text{not } X) \text{ or } Y |
| X \Rightarrow Y | (\text{not } Y) \Rightarrow (\text{not } X) |
| X \Leftrightarrow Y | (X \Rightarrow Y) \text{ and } (Y \Rightarrow X) |
| X \Leftrightarrow Y | (X \text{ and } Y) \text{ or (not } X \text{ and not } Y) |
| X \text{ xor } Y | (X \text{ and not } Y) \text{ or (not } X \text{ and } Y) |
| \text{not } (X \Rightarrow Y) | X \text{ and not } Y |
| \text{not } (X \Leftrightarrow Y) | X \text{ xor } Y |
| \text{not } (X \text{ xor } Y) | X \Leftrightarrow Y |
Analogické zákony jako při počítání s čísly
Pro logické operace and a or také platí komutativní (1. a 2. řádek následující tabulky), asociativní (3. a 4. řádek) a distributivní zákony (5. a 6. řádek):
| Výrok | Ekvivalentní výrok |
|---|---|
| X \text{ and } Y | Y \text{ and } X |
| X \text{ or } Y | Y \text{ or } X |
| (X \text{ and }Y) \text{ and } Z | X \text{ and } (Y \text{ and }Z) |
| (X \text{ or } Y) \text{ or } Z | X \text{ or } (Y \text{ or } Z) |
| X \text{ and } (Y \text{ or } Z) | (X \text{ and } Y) \text{ or } (X \text{ and } Z) |
| X \text{ or } (Y \text{ and } Z) | (X \text{ or } Y) \text{ and } (X \text{ or } Z) |
Další cvičení s trochu jinou notací najdete i na umíme matiku.
NahoruLogické odvozování s výrazy
Logické odvozování s pomocí logických výrazů je formální varianta odvozování logických důsledků slovy.
Jde o proces, kdy dostaneme několik logických výrazů (faktů) a odvozujeme z nich jiný výraz (závěr). Nemusíme ale nutně jen odvozovat nové závěry, můžeme se i například pokoušet rozhodnout, jestli nějaký dodaný výrok plyne z jiných.
Říkáme, že výraz se dá odvodit (tedy vyplývá) ze zadaných výrazů právě tehdy, když platí ve všech případech, kdy platí všechny zadané výrazy.
Příklady
- Z výrazu X \text{ and } Y můžeme odvodit X, protože kdykoli platí X \text{ and } Y, musí platit X i Y, a tím spíš musí platit i samotné X.
- Z výrazů X \text{ or } Y a \text{not } X můžeme odvodit Y. Aby bylo splněno X \text{ or } Y, musí platit X nebo Y, ale X platit nemůže. Proto platí Y.
- Z výrazů X \Leftrightarrow Y a X můžeme odvodit Y. Výraz X \Leftrightarrow Y říká, že Y má vždy stejnou hodnotu jako X. Z pravdivosti X tak můžeme odvodit pravdivost Y.
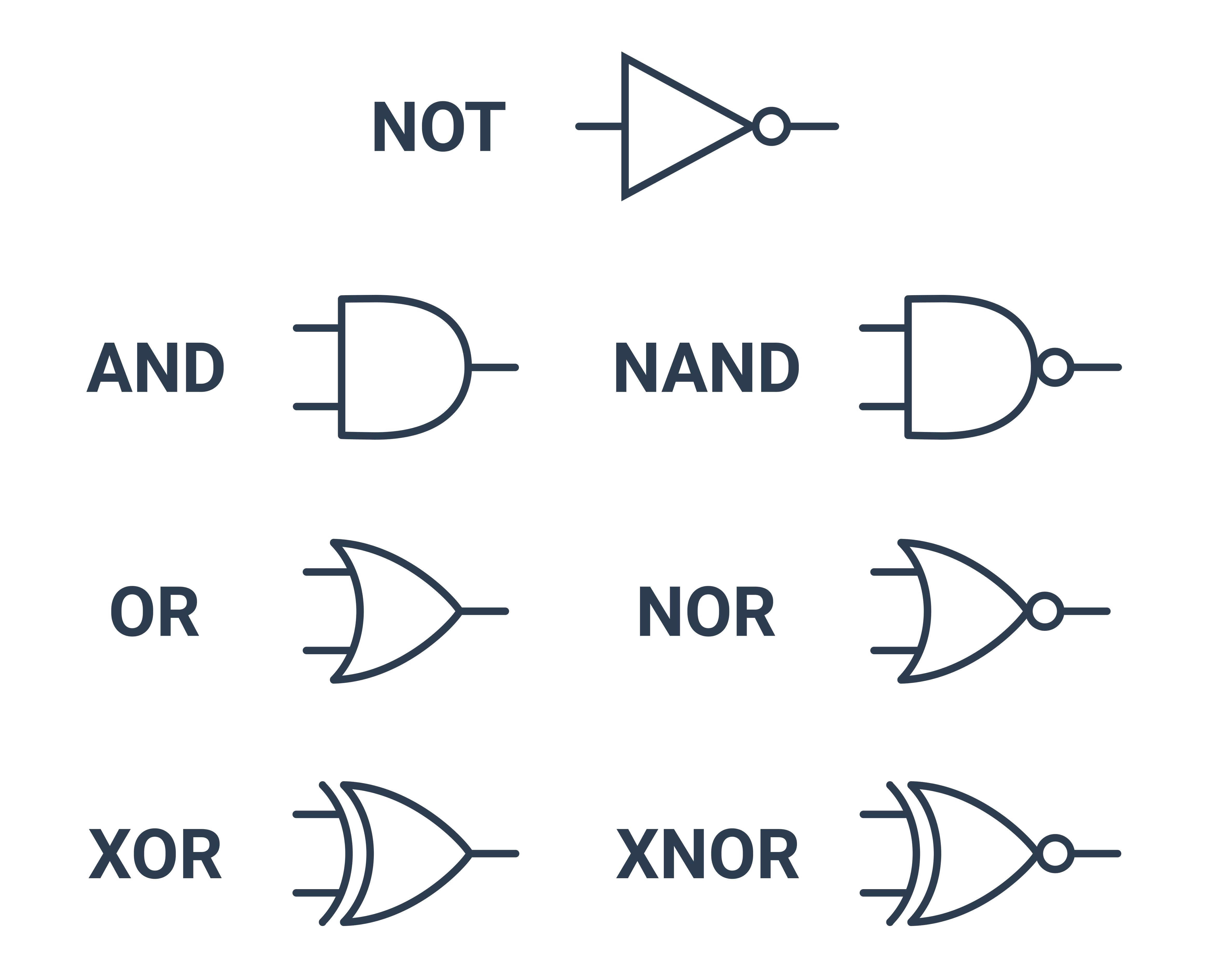
Značky logických bran a obvody
Logické spojky jsou v počítači reprezentovány součástkami, kterým se říká logické brány. Z logických bran se pak dají skládat složitější logické obvody, které dokáží například sčítat nebo násobit čísla.
Příklady logických bran


 Čeština
Čeština Matematika
Matematika Angličtina
Angličtina Biologie
Biologie Němčina
Němčina Umíme to
Umíme to Zeměpis
Zeměpis Chemie
Chemie Dějepis
Dějepis Fyzika
Fyzika ZSV
ZSV