Výpis souhrnů
Funkce a zobecňování
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Funkce a zobecňování
Funkce jsou základním stavebním blokem, pomocí kterého vytváříme programy. Představují konkrétní realizaci obecného principu rozklad na části.
Zjednodušeně řečeno, funkce je kouzlo, kterému něco předložíme (vstup) a ono nám vykouzlí něco jiného (výstup).
- Pohádkový příklad: Zvětšovací kouzelná hůlka, kterou poťukáme zeleninu a ona ji zvětší na dvakrát větší velikost.
- Matematický příklad: Funkce odmocnina, která dáme na vstup číslo a ona nám vrátí jiné číslo (např. pro vstup 25, vrátí výsledek 5).
- Programátorský příklad: Funkce
polygon(n, délka), které dáme na vstup dvě čísla (počet stran a délku strany) a ona vykreslí obrázek mnohoúhelníku.
Jednoduché funkce bez parametrů umožňují pouze opakované vykonání přesně téhož kódu (např. vždy stejně velký čtverec). Funkce však mohou obsahovat i parametry, které ovlivňují jejich chování (např. velikost čtverce). Funkce mohou volat jiné funkce a někdy dokonce samy sebe – takovým funkcím se říká rekurzivní.
Při zavádění funkcí potřebujeme umět abstrahovat – tedy odhlédnout od nepodstatných detailů – a následně kód zobecnit – tedy nahradit proměnlivé detaily proměnnými, z nichž pak uděláme parametry funkce. Složitý program, zejména takový, ve kterém se opakuje podobný kód, lze rozložit do několika funkcí, a tím ho zjednodušit a zpřehlednit.
NahoruAbstrakce
Abstrakce je schopnost odhlížet od detailů, které nejsou důležité pro řešení zkoumaného problému. Soustředíme se na společné prvky a vlastnosti, pomocí kterých nacházíme obecnější řešení.
Příklad z běžného života: Alík, Ben a Rex jsou tři konkrétní domácí zvířata. Můžeme je označit abstraktním pojmem „pes“ – tím zanedbáváme řadu jejich vlastností (např. stáří, barvu srsti či rasu) a soustředíme se jen na to, co mají společné. Kdybychom měli doma ještě kocoura Mourka, tak bychom mohli pro jejich společné označení použít třeba kategorii „savec“.
Příklad z programování: Při vykreslování obrázků můžeme vytvořit funkci squareA(), která vykreslí modrý čtverec o velikosti 100, a squareB(), která vykreslí žlutý čtverec o velikosti 200. Lepší je ale vytvořit abstraktnější funkci square(length, color), která vykreslí čtverec libovolné velikosti a barvy (podle zadaných parametrů). Případně můžeme v abstrakci pokračovat dál a vytvořit funkci, která vykreslí libovolný mnohoúhelník (se zadaným počtem vrcholů).
Funkce bez parametrů
Funkce je pojmenovaný blok kódu, který slouží k provedení nějakého úkolu (např. výpočet obsahu, nakreslení čtverce). Funkci provedeme (tzv. „zavoláme“) jejím jménem:

Funkce v programování a matematice
Funkce v programování a v matematice jsou podobné koncepty. Funkce v matematice (např. druhá mocnina) předepisuje, jak se nějaká hodnota změní na jinou (např. 3 → 9). Podobně funkce v programování může provádět výpočty (např. počítat druhou mocninu), může ale také třeba něco vykreslit nebo vypsat. Druhý rozdíl spočívá v tom, že součástí definice funkce v programování musí být přesný postup (posloupnost kroků), jak výsledku dosáhnout. (Některé matematické funkce přitom nelze spočítat žádným programem.)
Funkce ve Scratchi
I ve Scratchi si můžete definovat vlastní funkce (nové bloky). Označují se jako scénáře a najdete je v sekci Moje bloky.
Definice a volání funkce
Definice funkce zahrnuje její jméno a tělo – blok kódu, který se má provést, když funkci zavoláme. Funkce se neprovede při její definici, ale až poté, co ji zavoláme. Funkci definujeme jednou a můžeme ji pak volat opakovaně.
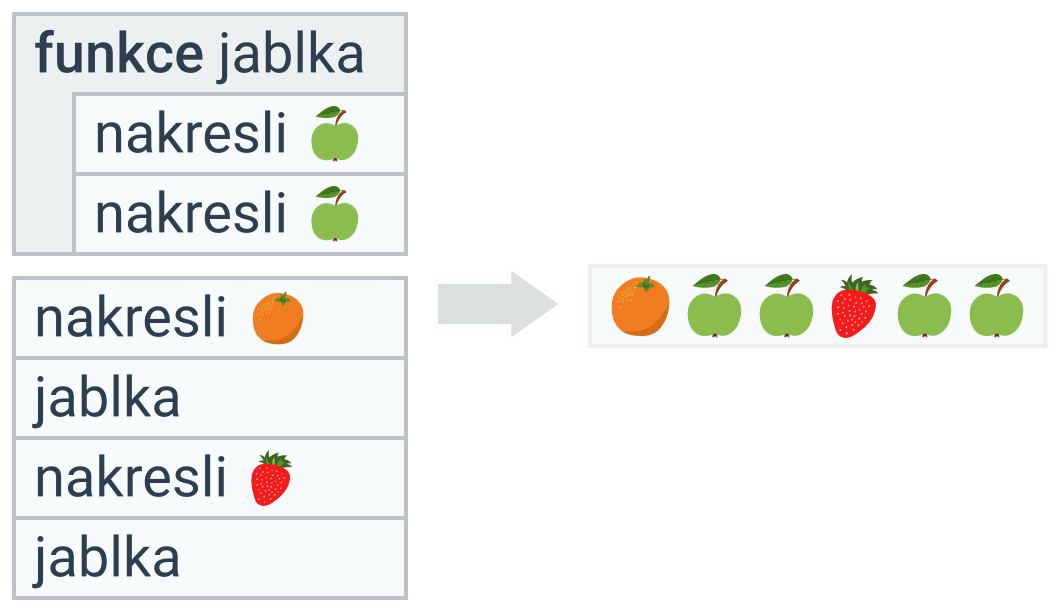
Funkce mohou obsahovat i parametry, které ovlivňují jejich chování (např. velikost čtverce), v této kapitole se však omezíme na jednoduché funkce bez parametrů.
Využití funkcí
Funkce nám umožňují definovat si vlastní příkazy (bloky), nebo využít příkazy, které napsal někdo jiný. Pokud řešíme složitý problém, můžeme ho zjednodušit rozložením na podproblémy, které vyřešíme zvlášť – každý podproblém pomocí jedné funkce, která je jednodušší než program pro celý problém. Pokud se nám v programu opakuje podobný kód, můžeme ho zavedením funkce pro opakující se úsek kódu zkrátit. Kód, který je strukturovaný do funkcí a který neobsahuje podobný kód na více místech, se pak snáze čte, opravuje a rozšiřuje.
NahoruFunkce s parametry
Funkce mohou mít parametry, které ovlivňují jejich chování. To se hodí pro psaní obecných funkcí, které budou použitelné ve více případech – různé hodnoty parametrů povedou na různé chování. Parametry se většinou zapisují do závorek za jméno funkce. Když funkci voláme, musíme dodat hodnoty parametrů (opět typicky v závorkách za jménem funkce).
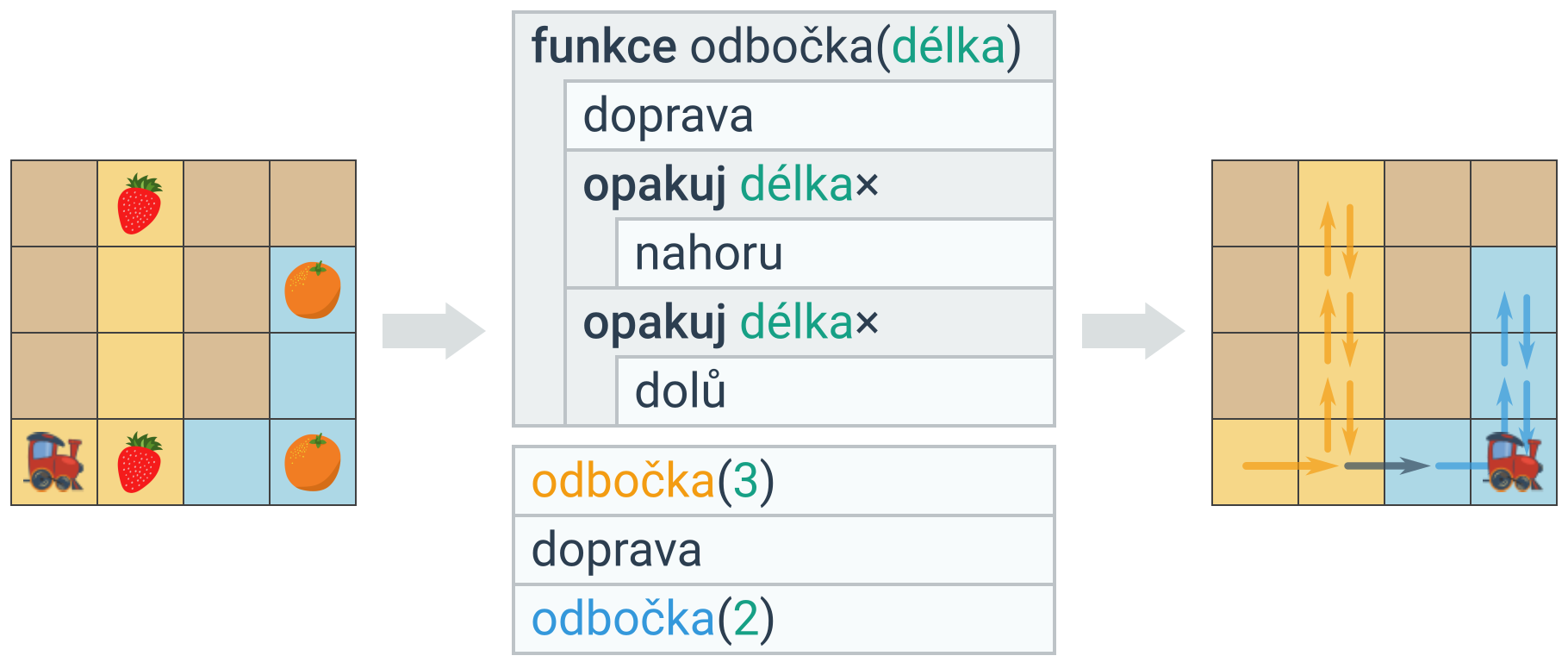
Parametry funkce lze vnímat jako speciální proměnné. Předaným hodnotám parametrů se říká argumenty. (V ukázce výše je parametrem jméno délka, zatímco čísla 3 a 2 argumenty.)
Parametry ve Scratchi
Scratch označuje funkce jako „scénáře“ či „moje bloky“ a umožňuje jim přiřadit parametry různých typů – číslo, text, logická hodnota (pravda/nepravda).
Více parametrů
Funkce může mít parametrů více. Oddělují se většinou čárkou. První parametr se nastaví na první předaný argument, druhý parametr na druhý předaný argument atd. V následující ukázce se nastaví n = 5, x = 3 a vypíše se pět trojek. Pokud bychom volali řada(3, 5) nastavilo by se n = 3, x = 5 a vypsaly by se tři pětky.

Funkce s návratovou hodnotou
Funkce mohou vracet vypočtenou hodnotu pomocí klíčového slova vrať. Takové funkce pak lze využít v rámci výrazů, resp. všude, kde se očekává nějaká hodnota. V následující ukázce lze využít funkci mocnina při volání funkce smích, protože mocnina(3) vrací hodnotu 9. Kdyby funkce mocnina výsledek vypisovala, ale nevracela, nebylo by toto možné.
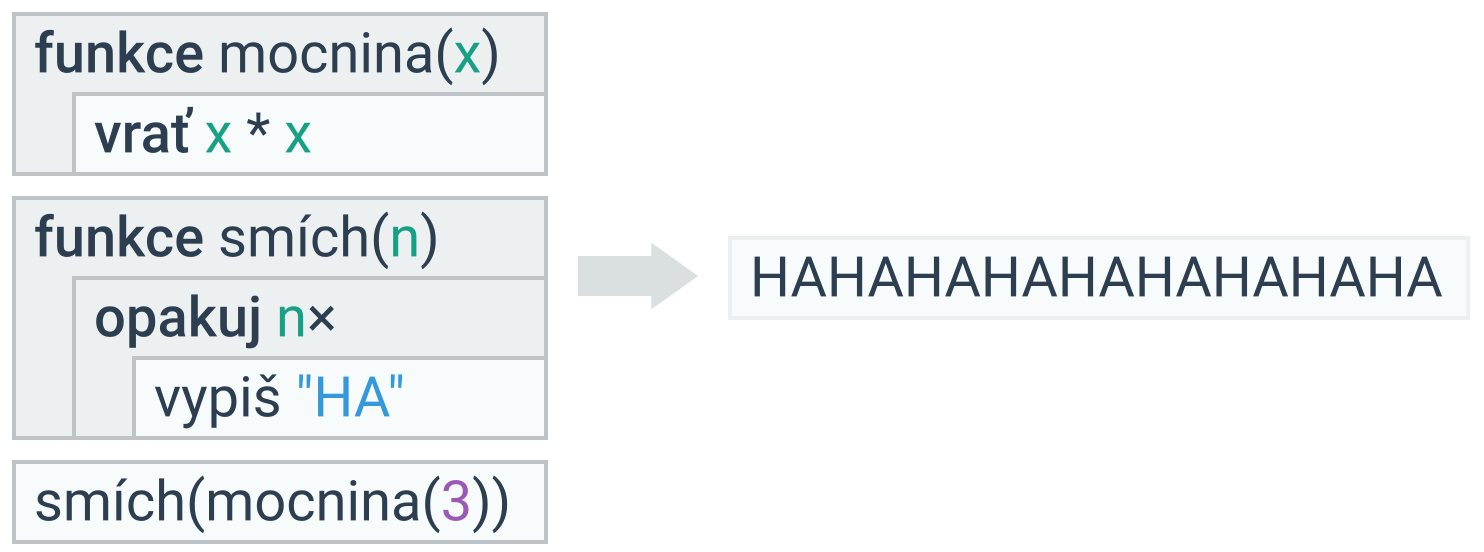
Funkce vs. procedury
Někdy se rozlišuje mezi funkcemi, které vrací hodnotu, a procedurami, které nic nevrací. Obecný název pro funkce a procedury je pak podprogram. Často se však mezi těmito případy nerozlišuje a používá se pouze pojem „funkce“.
Zobecňování programů
Programy lze často zobecnit (abstrahovat) nahrazením konkrétní hodnoty za obecnou proměnnou. To umožňuje tvořit programy, které řeší obecnější problémy. Například místo několika různých programů pro výpis čísla obklopeného jedničkami stačí jediný: 

Při zobecňování je někdy potřeba kromě proměnné zavést také podmíněný příkaz nebo cyklus. Příklad:


Kromě vytváření obecnějších řešení můžeme pomocí zobecňování upravovat programy tak, aby byly přehlednější. Když si v programu všimneme opakujícího se vzoru (např. opakované výpisy čísla obklopeného jedničkami), můžeme tyto kousky kódu po vhodném zobecnění nahradit společnou funkcí (parametrizovanou proměnnými zavedenými při zobecňování).
NahoruRozklad programů
Složitý program lze zpřehlednit tím, že ho rozdělíme na několik částí, které vyčleníme do samostatných funkcí. V takovém programu se navíc snáze hledají a opravují chyby, protože můžeme testovat jednotlivé funkce zvlášť.
Příklad: V následujícím programu je výpis posloupnosti 11–14 podobný výpisu posloupnosti 31–34. V obou případech jde o výpis 4 čísel od n+1 do n+4. Můžeme proto tyto výpisy nahradit voláním nové funkce s parametrem n, která bude vypisovat n+1 až n+4.


Program rozdělujeme tak, aby nově zavedené funkce měly jasný význam. Často pomůže všimnout si částí programu, které si jsou hodně podobné (hledání vzorů). Tyto části zobecníme tak, aby je vykonával stejný kód a ten zapíšeme do nové funkce (jejími parametry jsou proměnné potřebné ke společnému zobecnění kódů). Původní kódy pak nahradíme voláním této nové funkce.
NahoruRekurze je využití sebe sama. Příkladem je použití pojmu při jeho vlastní definici nebo obrázek obsahující svoji zmenšenou kopii. Rekurzivní funkce je taková funkce, která pro výpočet využívá sebe sama (s jinými hodnotami parametrů). Využití rekurze často vede k elegantnímu řešení problému. Některé programovací jazyky využívají rekurzi jako základní prostředek pro opakování příkazů (místo cyklů).
Faktoriál – příklad rekurzivní definice
Faktoriál čísla n (značí se n!) je součin čísel 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n. Například 4! = 1 \cdot 2 \cdot 3 \cdot 4 = 24. Faktoriál lze definovat rekurzivně:
0! = 1
n! = n \cdot (n - 1)! \text{ pro } n > 0
Nejedná se o definici v kruhu, protože při aplikování definice dochází ke zjednodušování (faktoriál n je definován pomocí faktoriálu n - 1) a je definován i bázový případ (n = 0) bez rekurze, ke kterému vše směřuje. Jde tedy spíše o definici ve spirále.
Rekurzivní šroubování žárovky
A: Kolik otoček potřebuji na zašroubování žárovky?
B: Pokud už je zašroubovaná, tak 0. Jinak ji zatoč jednou, zeptej se mě znova a k mé odpovědi přičti 1.
Návrh rekurzivních algoritmů
Nejprve určíme podproblémy, které potřebujeme k vyřešení našeho problému (např. pro výpočet faktoriálu n potřebujeme znát faktoriál n - 1). Tyto podproblémy vyřešíme rekurzivně (tedy voláním funkce s jinými parametry) a z výsledků poskládáme výsledné řešení. Dále je nutné určit bázový případ a jeho řešení (např. faktoriál 0 je 1). Bázový případ musí být takový, aby se k němu všechny větve výpočtu časem dostaly, jinak by výpočet nikdy neskončil.
Sebe-reference
Rekurze je příkladem obecnějšího jevu odkazování na sebe sama, tzv. sebe-reference. Sebe-reference se vyskytuje v jazyce (Třeba tato věta mluví sama o sobě.), knihách, divadle, filmu i matematice. Sebe-reference je dokonce hlavní ingrediencí snad nejslavnějších důkazů matematiky (Gödelovy věty o neúplnosti) a také informatiky (existence problémů, pro které neexistuje algoritmus, který by je řešil – např. úloha určit, zda daný program někdy zastaví).
Fraktály
Vedle rekurze jsou nejtypičtějším zástupcem sebe-reference fraktály – obrázky, které jsou soběpodobné, tedy jejich části připomínají obrázek jako celek. Fraktály lze často vidět v přírodě (např. větve stromů, kapradina). Fraktály a rekurze nejsou dva nezávislí reprezentanti sebe-reference, i mezi nimi je silná souvislost. Rekurze je totiž velmi elegantní způsob, jak různé fraktály definovat. Díky tomu často můžeme složité fraktály vykreslit pomocí jednoduchých rekurzivních funkcí.
Nahoru

 Čeština
Čeština Matematika
Matematika Angličtina
Angličtina Biologie
Biologie Němčina
Němčina Umíme to
Umíme to Zeměpis
Zeměpis Chemie
Chemie Dějepis
Dějepis Fyzika
Fyzika ZSV
ZSV